Annotation
- Introduction
- Understanding Laplacian Gaussian Edge Detection
- Mathematical Foundation of LoG
- Practical Implementation with Python and OpenCV
- Zero-Crossing Detection Methodology
- Parameter Optimization Strategies
- Advanced Implementation Considerations
- Real-World Applications and Use Cases
- Comparison with Alternative Edge Detection Methods
- Pros and Cons
- Conclusion
- Frequently Asked Questions
Laplacian Gaussian Edge Detection: Implementation Guide & Python Code
This comprehensive guide covers Laplacian of Gaussian edge detection, from mathematical foundations to Python implementation with OpenCV, including

Introduction
Edge detection represents a fundamental pillar in computer vision, enabling machines to interpret visual data by identifying boundaries and transitions within images. Among the sophisticated techniques available, the Laplacian of Gaussian (LoG) method stands out for its unique approach to balancing noise reduction with precise edge localization. This comprehensive guide explores LoG's mathematical foundations, practical implementation strategies, and optimization techniques for real-world applications across various domains including medical imaging and object recognition systems.
Understanding Laplacian Gaussian Edge Detection
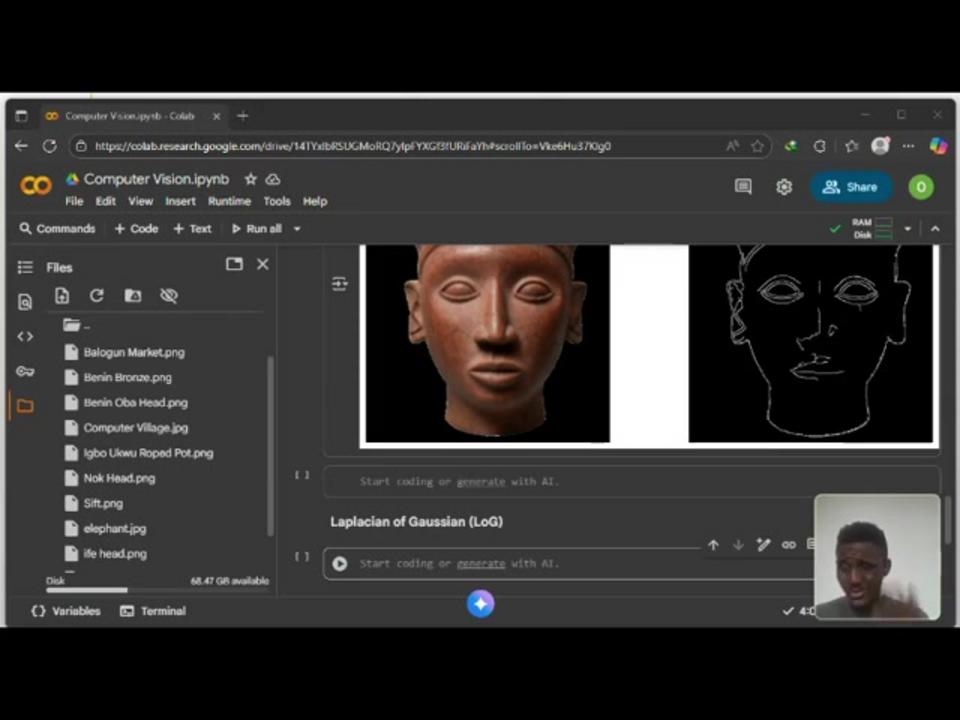
The Laplacian of Gaussian (LoG) operates as a sophisticated second-order derivative edge detector that strategically combines two powerful mathematical operations. This dual approach addresses one of the primary challenges in edge detection: distinguishing genuine image features from random noise artifacts. The technique begins by applying a Gaussian filter to smooth the input image, effectively suppressing high-frequency noise that could otherwise trigger false edge detections. This preprocessing step creates a cleaner foundation for the subsequent Laplacian operation, which enhances regions of rapid intensity change – the very definition of edges in digital imagery.
What makes LoG particularly effective is its zero-crossing detection mechanism. After the combined filtering and differentiation process, the algorithm identifies points where the processed image values transition from positive to negative or vice versa. These zero-crossing locations correspond precisely to edge positions in the original image. This methodology proves especially valuable when working with inherently noisy data sources, such as medical scans or low-light photography, where traditional edge detectors might struggle with accuracy. For those exploring various AI image generators, understanding these fundamental computer vision techniques provides valuable insight into how artificial intelligence processes visual information.
Mathematical Foundation of LoG
The mathematical elegance of LoG lies in its combination of two well-established operations. The Gaussian filtering component employs a two-dimensional Gaussian function defined as G(x, y) = (1/(2πσ²)) × e^(-(x²+y²)/(2σ²)), where σ represents the standard deviation controlling the degree of smoothing. This Gaussian kernel creates a weighted average of pixel neighborhoods, with closer pixels contributing more significantly to the result than distant ones.
The Laplacian operator then applies second-order differentiation to this smoothed image. Mathematically expressed as ∇²f = ∂²f/∂x² + ∂²f/∂y², this operation highlights regions where intensity changes rapidly. The combined LoG kernel emerges as the Laplacian of the Gaussian function: LoG(x, y) = ∇²G(x, y) = -(1/(πσ⁴)) × [1 - (x²+y²)/(2σ²)] × e^(-(x²+y²)/(2σ²)). This sophisticated kernel simultaneously performs smoothing and edge enhancement through convolution, where the kernel slides across the image, multiplying and summing values to produce the filtered output. This mathematical approach ensures isotropic response, meaning edges are detected consistently regardless of their orientation within the image.
Practical Implementation with Python and OpenCV
Implementing LoG edge detection requires setting up a proper development environment with essential libraries. The core implementation relies on OpenCV for image processing operations and NumPy for numerical computations. Begin by installing these dependencies using pip install opencv-python numpy matplotlib. Once configured, the implementation follows a straightforward workflow that begins with image loading and preprocessing.
The Python implementation centers around a custom function that applies Gaussian blurring followed by the Laplacian operator. Critical parameters include kernel_size, which determines the neighborhood size for blurring operations, and sigma, controlling the spread of the Gaussian filter. Larger kernel sizes and higher sigma values produce more aggressive smoothing, which benefits noisy images but may compromise fine detail preservation. The data type specification (cv2.CV_64F) ensures proper handling of negative values during Laplacian computation, which is essential for accurate zero-crossing detection later in the process.
For developers working with various photo editor tools, understanding these underlying algorithms provides deeper insight into how professional image processing software achieves its results. The visualization component using matplotlib allows for immediate feedback on parameter adjustments, facilitating an iterative optimization process.
Zero-Crossing Detection Methodology
Zero-crossing detection represents the final and most critical phase in LoG edge detection. This process identifies the precise locations where the filtered image transitions between positive and negative values, corresponding to edge positions. The implementation involves scanning the LoG-processed image and examining pixel neighborhoods for sign changes. A comprehensive approach checks multiple directions – horizontal, vertical, and both diagonals – to ensure no edge orientation is missed.
The algorithm creates a binary output image where detected zero-crossings are marked while other regions remain dark. This clean representation simplifies subsequent processing steps and provides a clear visualization of detected edges. However, this process can be computationally intensive, particularly for high-resolution images, making optimization considerations important for real-time applications. Techniques like neighborhood pruning and efficient memory access patterns can significantly improve performance without compromising detection accuracy.
Parameter Optimization Strategies
Successful LoG implementation hinges on appropriate parameter selection, primarily kernel_size and sigma values. These parameters exist in a delicate balance – larger values enhance noise reduction but risk excessive blurring that obscures genuine edges, while smaller values preserve detail but may inadequately suppress noise. A systematic approach to parameter tuning involves testing multiple combinations across representative image samples.
For standard applications, starting with kernel_size=5 and sigma=1.4 provides a reasonable baseline. Images with higher noise levels may benefit from increased values (kernel_size=7, sigma=2.0), while high-detail images might require more conservative settings (kernel_size=3, sigma=0.8). The optimal configuration often depends on specific application requirements, whether prioritizing edge precision or noise immunity. Many professional screen capture tools incorporate similar parameter adjustment capabilities, allowing users to balance clarity and detail in their processed images.
Advanced Implementation Considerations
Beyond basic implementation, several advanced considerations can enhance LoG performance. Thresholding represents a valuable post-processing step that filters weak edges by establishing minimum intensity requirements. This helps eliminate spurious detections while preserving structurally significant edges. Additionally, morphological operations like dilation can connect discontinuous edge fragments, creating more continuous boundaries that better represent object contours.
Computational efficiency becomes crucial when processing large image datasets or operating in real-time environments. Optimization strategies include using separable Gaussian kernels that decompose 2D convolution into sequential 1D operations, significantly reducing computational complexity. Hardware acceleration through GPU processing or specialized image processing libraries can provide substantial performance improvements. For those working with various image converter applications, these optimization techniques demonstrate how algorithmic efficiency translates to practical performance benefits.
Real-World Applications and Use Cases
LoG edge detection finds application across numerous domains where precise boundary identification is crucial. In medical imaging, it helps delineate anatomical structures in MRI and CT scans, assisting in diagnosis and treatment planning. Industrial inspection systems utilize LoG to detect defects in manufactured products by identifying irregularities in surface patterns. Autonomous vehicles rely on similar edge detection techniques to interpret road boundaries and obstacle contours from camera feeds.
The methodology also proves valuable in scientific image analysis, where researchers extract features from microscopic images or astronomical observations. Even in creative fields, understanding these algorithms enhances work with various diagram creator tools and digital art applications. The technique's robustness against noise makes it particularly suitable for challenging imaging conditions where other methods might fail, establishing LoG as a versatile tool in the computer vision toolkit.
Comparison with Alternative Edge Detection Methods
When evaluating edge detection techniques, LoG occupies a distinctive position between simpler gradient-based methods and more complex algorithms. Compared to first-order operators like Sobel or Prewitt, LoG provides superior noise immunity but requires more computational resources. Against the sophisticated Canny edge detector, LoG offers implementation simplicity while sacrificing some of Canny's flexibility and hysteresis thresholding capabilities.
The choice between methods often depends on specific application requirements. LoG excels in scenarios where mathematical elegance, predictable behavior, and moderate noise resistance are prioritized over ultimate detection precision. Its single-operator approach appeals to applications requiring straightforward implementation without extensive parameter tuning. For users of various color picker tools, understanding these algorithmic differences illuminates how software extracts and processes visual information at fundamental levels.
Pros and Cons
Advantages
- Excellent noise reduction through Gaussian preprocessing
- Isotropic response detects edges in all orientations equally
- Combined operator simplifies implementation workflow
- Clear zero-crossing representation facilitates edge localization
- Effective balance between smoothing and edge enhancement
- Proven reliability across diverse image types and domains
- Mathematically well-founded with predictable behavior
Disadvantages
- Excessive blurring can obscure fine details with large kernels
- Parameter sensitivity requires careful tuning for optimal results
- Computationally intensive for high-resolution images
- May underperform compared to Canny in complex scenarios
- Zero-crossing detection adds processing overhead
Conclusion
The Laplacian of Gaussian edge detection method represents a sophisticated approach that elegantly balances noise reduction with precise edge localization. Through its combination of Gaussian smoothing and Laplacian differentiation, LoG addresses fundamental challenges in computer vision while maintaining mathematical transparency and predictable behavior. The technique's versatility across medical, industrial, and research applications demonstrates its enduring value in the image processing toolkit. While parameter sensitivity and computational demands present implementation challenges, the method's robust performance in noisy environments and consistent edge detection across orientations ensure its continued relevance. As computer vision technologies advance, understanding foundational algorithms like LoG provides crucial insight into both current capabilities and future developments in automated image analysis and interpretation.
Frequently Asked Questions
What is the main advantage of LoG over basic Laplacian edge detection?
LoG's primary advantage is noise reduction through Gaussian preprocessing, which smooths the image before edge detection, making it more robust against random noise artifacts compared to the basic Laplacian operator.
How does sigma parameter affect LoG edge detection results?
Sigma controls the Gaussian blur intensity - higher values increase smoothing for better noise reduction but may blur fine edges, while lower values preserve details but offer less noise immunity.
Can LoG edge detection work in real-time applications?
Yes, with optimizations like separable kernels, GPU acceleration, and efficient zero-crossing detection, LoG can achieve real-time performance for moderate resolution images in suitable hardware environments.
What are zero-crossing points in LoG detection?
Zero-crossing points are locations where the LoG-filtered image changes sign from positive to negative or vice versa, corresponding precisely to edge positions in the original image.
When should I use LoG instead of other edge detectors like Canny?
Use LoG when you need a balance of noise reduction and edge localization with simpler implementation, especially in noisy environments, but choose Canny for better edge connectivity in complex scenes.