Détection de bords Laplacien Gaussien : Guide d'implémentation et code Python

Introduction

La détection des contours représente un pilier fondamental en vision par ordinateur, permettant aux machines d'interpréter les données visuelles en identifiant les limites et les transitions dans les images. Parmi les techniques sophistiquées disponibles, la méthode du Laplacien du Gaussien (LoG) se distingue par son approche unique pour équilibrer la réduction du bruit avec la localisation précise des contours. Ce guide complet explore les fondements mathématiques du LoG, les stratégies de mise en œuvre pratiques et les techniques d'optimisation pour les applications réelles dans divers domaines, y compris l'imagerie médicale et les systèmes de reconnaissance d'objets.

Comprendre la détection des contours par Laplacien du Gaussien

Le Laplacien du Gaussien (LoG) fonctionne comme un détecteur de contours sophistiqué de dérivée seconde qui combine stratégiquement deux opérations mathématiques puissantes. Cette double approche aborde l'un des principaux défis de la détection des contours : distinguer les véritables caractéristiques de l'image des artefacts de bruit aléatoire. La technique commence par appliquer un filtre gaussien pour lisser l'image d'entrée, supprimant efficacement le bruit haute fréquence qui pourrait autrement déclencher de fausses détections de contours. Cette étape de prétraitement crée une base plus propre pour l'opération laplacienne suivante, qui améliore les régions de changement rapide d'intensité – la définition même des contours dans l'imagerie numérique.

Ce qui rend le LoG particulièrement efficace est son mécanisme de détection de passage par zéro. Après le processus combiné de filtrage et de différenciation, l'algorithme identifie les points où les valeurs de l'image traitée passent du positif au négatif ou vice versa. Ces emplacements de passage par zéro correspondent précisément aux positions des contours dans l'image originale. Cette méthodologie s'avère particulièrement précieuse lorsqu'on travaille avec des sources de données intrinsèquement bruyantes, comme les scanners médicaux ou la photographie en faible luminosité, où les détecteurs de contours traditionnels pourraient avoir des difficultés de précision. Pour ceux qui explorent divers générateurs d'images IA, comprendre ces techniques fondamentales de vision par ordinateur fournit un aperçu précieux de la façon dont l'intelligence artificielle traite les informations visuelles.

Fondement mathématique du LoG

L'élégance mathématique du LoG réside dans sa combinaison de deux opérations bien établies. La composante de filtrage gaussien utilise une fonction gaussienne bidimensionnelle définie comme G(x, y) = (1/(2πσ²)) × e^(-(x²+y²)/(2σ²)), où σ représente l'écart type contrôlant le degré de lissage. Ce noyau gaussien crée une moyenne pondérée des voisinages de pixels, les pixels plus proches contribuant plus significativement au résultat que les pixels éloignés.

L'opérateur laplacien applique ensuite une différenciation de second ordre à cette image lissée. Exprimé mathématiquement comme ∇²f = ∂²f/∂x² + ∂²f/∂y², cette opération met en évidence les régions où l'intensité change rapidement. Le noyau LoG combiné émerge comme le Laplacien de la fonction gaussienne : LoG(x, y) = ∇²G(x, y) = -(1/(πσ⁴)) × [1 - (x²+y²)/(2σ²)] × e^(-(x²+y²)/(2σ²)). Ce noyau sophistiqué effectue simultanément le lissage et l'amélioration des contours par convolution, où le noyau glisse à travers l'image, multipliant et sommant les valeurs pour produire la sortie filtrée. Cette approche mathématique assure une réponse isotrope, ce qui signifie que les contours sont détectés de manière cohérente quelle que soit leur orientation dans l'image.

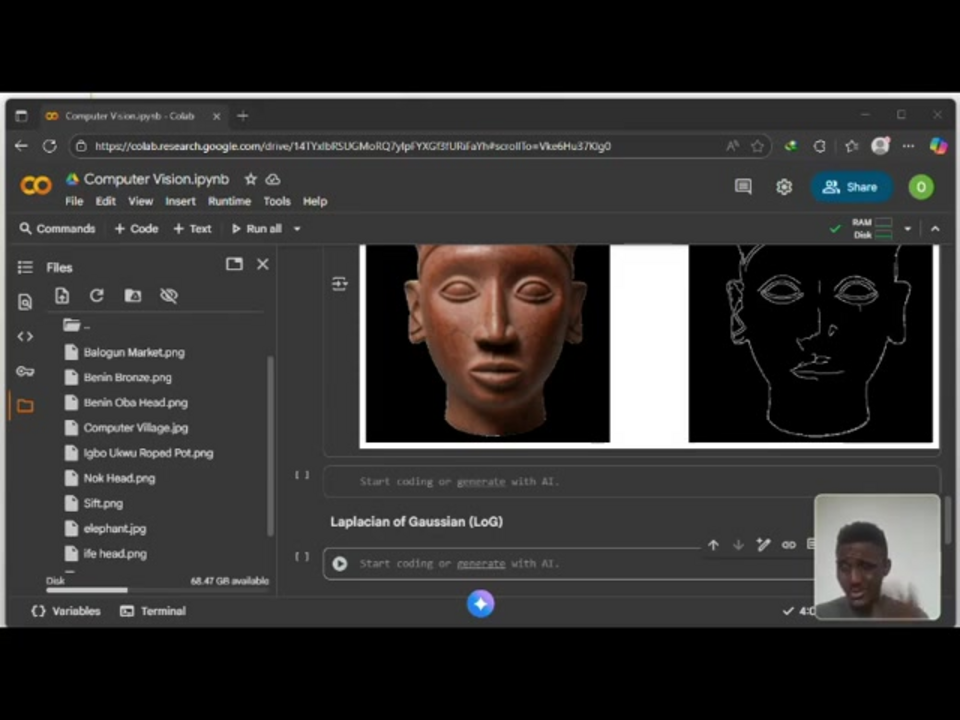
Mise en œuvre pratique avec Python et OpenCV

La mise en œuvre de la détection des contours LoG nécessite la configuration d'un environnement de développement approprié avec des bibliothèques essentielles. L'implémentation principale repose sur OpenCV pour les opérations de traitement d'image et NumPy pour les calculs numériques. Commencez par installer ces dépendances en utilisant pip install opencv-python numpy matplotlib. Une fois configuré, la mise en œuvre suit un flux de travail simple qui commence par le chargement et le prétraitement de l'image.

L'implémentation en Python se centre autour d'une fonction personnalisée qui applique un flou gaussien suivi de l'opérateur laplacien. Les paramètres critiques incluent kernel_size, qui détermine la taille du voisinage pour les opérations de flou, et sigma, contrôlant l'étalement du filtre gaussien. Des tailles de noyau plus grandes et des valeurs sigma plus élevées produisent un lissage plus agressif, ce qui bénéficie aux images bruyantes mais peut compromettre la préservation des détails fins. La spécification du type de données (cv2.CV_64F) assure une manipulation correcte des valeurs négatives pendant le calcul laplacien, ce qui est essentiel pour une détection précise du passage par zéro plus tard dans le processus.

Pour les développeurs travaillant avec divers outils d'édition photo, comprendre ces algorithmes sous-jacents fournit un aperçu plus profond de la façon dont les logiciels professionnels de traitement d'image obtiennent leurs résultats. La composante de visualisation utilisant matplotlib permet un retour immédiat sur les ajustements des paramètres, facilitant un processus d'optimisation itératif.

Méthodologie de détection du passage par zéro

La détection du passage par zéro représente la phase finale et la plus critique dans la détection des contours LoG. Ce processus identifie les emplacements précis où l'image filtrée transitionne entre des valeurs positives et négatives, correspondant aux positions des contours. La mise en œuvre implique de scanner l'image traitée par LoG et d'examiner les voisinages de pixels pour les changements de signe. Une approche complète vérifie plusieurs directions – horizontale, verticale et les deux diagonales – pour s'assurer qu'aucune orientation de contour n'est manquée.

L'algorithme crée une image de sortie binaire où les passages par zéro détectés sont marqués tandis que les autres régions restent sombres. Cette représentation propre simplifie les étapes de traitement ultérieures et fournit une visualisation claire des contours détectés. Cependant, ce processus peut être intensif en calcul, particulièrement pour les images haute résolution, rendant les considérations d'optimisation importantes pour les applications en temps réel. Des techniques comme l'élagage des voisinages et des modèles d'accès mémoire efficaces peuvent significativement améliorer les performances sans compromettre la précision de détection.

Stratégies d'optimisation des paramètres

La mise en œuvre réussie du LoG dépend de la sélection appropriée des paramètres, principalement les valeurs de kernel_size et sigma. Ces paramètres existent dans un équilibre délicat – des valeurs plus grandes améliorent la réduction du bruit mais risquent un flou excessif qui obscurcit les véritables contours, tandis que des valeurs plus petites préservent les détails mais peuvent supprimer inadéquatement le bruit. Une approche systématique pour l'ajustement des paramètres implique de tester plusieurs combinaisons sur des échantillons d'images représentatifs.

Pour les applications standard, commencer avec kernel_size=5 et sigma=1.4 fournit une base raisonnable. Les images avec des niveaux de bruit plus élevés peuvent bénéficier de valeurs accrues (kernel_size=7, sigma=2.0), tandis que les images à haut détail pourraient nécessiter des réglages plus conservateurs (kernel_size=3, sigma=0.8). La configuration optimale dépend souvent des exigences spécifiques de l'application, qu'il s'agisse de prioriser la précision des contours ou l'immunité au bruit. De nombreux outils professionnels de capture d'écran intègrent des capacités similaires d'ajustement des paramètres, permettant aux utilisateurs d'équilibrer la clarté et le détail dans leurs images traitées.

Considérations avancées de mise en œuvre

Au-delà de l'implémentation de base, plusieurs considérations avancées peuvent améliorer les performances du LoG. Le seuillage représente une étape de post-traitement précieuse qui filtre les contours faibles en établissant des exigences minimales d'intensité. Cela aide à éliminer les détections erronées tout en préservant les contours structurellement significatifs. De plus, des opérations morphologiques comme la dilatation peuvent connecter des fragments de contours discontinus, créant des limites plus continues qui représentent mieux les contours des objets.

L'efficacité computationnelle devient cruciale lors du traitement de grands ensembles d'images ou de l'opération dans des environnements en temps réel. Les stratégies d'optimisation incluent l'utilisation de noyaux gaussiens séparables qui décomposent la convolution 2D en opérations 1D séquentielles, réduisant significativement la complexité computationnelle. L'accélération matérielle via le traitement GPU ou des bibliothèques spécialisées de traitement d'image peut fournir des améliorations substantielles de performance. Pour ceux qui travaillent avec diverses applications de conversion d'image, ces techniques d'optimisation démontrent comment l'efficacité algorithmique se traduit par des avantages de performance pratiques.

Applications et cas d'usage réels

La détection des contours LoG trouve des applications dans de nombreux domaines où l'identification précise des limites est cruciale. En imagerie médicale, elle aide à délimiter les structures anatomiques dans les IRM et les scanners, assistant au diagnostic et à la planification du traitement. Les systèmes d'inspection industrielle utilisent le LoG pour détecter les défauts dans les produits manufacturés en identifiant les irrégularités dans les motifs de surface. Les véhicules autonomes s'appuient sur des techniques similaires de détection des contours pour interpréter les limites de la route et les contours des obstacles à partir des flux de caméras.

La méthodologie s'avère également précieuse dans l'analyse d'images scientifiques, où les chercheurs extraient des caractéristiques d'images microscopiques ou d'observations astronomiques. Même dans les domaines créatifs, comprendre ces algorithmes améliore le travail avec divers outils de création de diagrammes et applications d'art numérique. La robustesse de la technique contre le bruit la rend particulièrement adaptée aux conditions d'imagerie difficiles où d'autres méthodes pourraient échouer, établissant le LoG comme un outil polyvalent dans la boîte à outils de vision par ordinateur.

Comparaison avec d'autres méthodes de détection des contours

Lors de l'évaluation des techniques de détection des contours, le LoG occupe une position distinctive entre les méthodes plus simples basées sur le gradient et les algorithmes plus complexes. Comparé aux opérateurs de premier ordre comme Sobel ou Prewitt, le LoG fournit une immunité au bruit supérieure mais nécessite plus de ressources computationnelles. Face au détecteur de contours sophistiqué de Canny, le LoG offre une simplicité de mise en œuvre tout en sacrifiant une partie de la flexibilité et des capacités de seuillage à hystérésis de Canny.

Le choix entre les méthodes dépend souvent des exigences spécifiques de l'application. Le LoG excelle dans les scénarios où l'élégance mathématique, le comportement prévisible et une résistance modérée au bruit sont prioritaires par rapport à la précision ultime de détection. Son approche à opérateur unique attire les applications nécessitant une mise en œuvre simple sans ajustement extensif des paramètres. Pour les utilisateurs de divers outils de sélection de couleurs, comprendre ces différences algorithmiques éclaire la façon dont le logiciel extrait et traite les informations visuelles à des niveaux fondamentaux.

Avantages et inconvénients

Avantages

• Excellente réduction du bruit grâce au prétraitement gaussien
• Réponse isotrope détecte les contours dans toutes les orientations de manière égale
• Opérateur combiné simplifie le flux de travail de mise en œuvre
• Représentation claire du passage par zéro facilite la localisation des contours
• Équilibre efficace entre lissage et amélioration des contours
• Fiabilité éprouvée à travers divers types d'images et domaines
• Fondement mathématique solide avec un comportement prévisible

Inconvénients

• Un flou excessif peut obscurcir les détails fins avec de grands noyaux
• La sensibilité aux paramètres nécessite un réglage minutieux pour des résultats optimaux
• Intensif en calcul pour les images haute résolution
• Peut sous-performer par rapport à Canny dans des scénarios complexes
• La détection du passage par zéro ajoute une surcharge de traitement

Conclusion

La méthode de détection des contours par Laplacien du Gaussien représente une approche sophistiquée qui équilibre élégamment la réduction du bruit avec la localisation précise des contours. Grâce à sa combinaison de lissage gaussien et de différenciation laplacienne, le LoG aborde les défis fondamentaux de la vision par ordinateur tout en maintenant une transparence mathématique et un comportement prévisible. La polyvalence de la technique à travers les applications médicales, industrielles et de recherche démontre sa valeur durable dans la boîte à outils de traitement d'image. Bien que la sensibilité aux paramètres et les demandes computationnelles présentent des défis de mise en œuvre, la performance robuste du LoG dans les environnements bruyants et la détection cohérente des contours à travers les orientations assurent sa pertinence continue. Alors que les technologies de vision par ordinateur avancent, comprendre les algorithmes fondamentaux comme le LoG fournit un aperçu crucial des capacités actuelles et des développements futurs dans l'analyse et l'interprétation automatisées des images.