拉普拉斯高斯边缘检测：实现指南与Python代码

介绍

边缘检测是计算机视觉中的一个基本支柱，使机器能够通过识别图像中的边界和过渡来解释视觉数据。在可用的复杂技术中，拉普拉斯高斯（LoG）方法因其在平衡噪声减少与精确边缘定位方面的独特方法而脱颖而出。本全面指南探讨了LoG的数学基础、实际实现策略以及优化技术，适用于包括医学成像和物体识别系统在内的各种领域的实际应用。

理解拉普拉斯高斯边缘检测

拉普拉斯高斯（LoG）作为一种复杂的二阶导数边缘检测器，策略性地结合了两种强大的数学操作。这种双重方法解决了边缘检测中的一个主要挑战：区分真实的图像特征与随机噪声伪影。该技术首先应用高斯滤波器平滑输入图像，有效抑制可能引发错误边缘检测的高频噪声。这一预处理步骤为后续的拉普拉斯操作创建了更清晰的基础，该操作增强了强度快速变化的区域——数字图像中边缘的确切定义。

使LoG特别有效的是其零交叉检测机制。在结合滤波和微分过程后，算法识别出处理后的图像值从正到负或反之过渡的点。这些零交叉位置精确对应原始图像中的边缘位置。这种方法在处理固有噪声数据源时尤其有价值，例如医学扫描或低光摄影，传统边缘检测器可能在此类场景中难以保证准确性。对于那些探索各种AI图像生成器的人来说，理解这些基础计算机视觉技术能提供关于人工智能如何处理视觉信息的宝贵见解。

LoG的数学基础

LoG的数学优雅在于它结合了两种成熟的操作。高斯滤波组件使用二维高斯函数，定义为G(x, y) = (1/(2πσ²)) × e^(-(x²+y²)/(2σ²))，其中σ代表控制平滑程度的标准差。该高斯核创建像素邻域的加权平均，较近的像素比远处的像素对结果贡献更显著。

拉普拉斯算子随后对这个平滑图像应用二阶微分。数学上表达为∇²f = ∂²f/∂x² + ∂²f/∂y²，此操作突出强度快速变化的区域。组合的LoG核作为高斯函数的拉普拉斯出现：LoG(x, y) = ∇²G(x, y) = -(1/(πσ⁴)) × [1 - (x²+y²)/(2σ²)] × e^(-(x²+y²)/(2σ²))。这个复杂核通过卷积同时执行平滑和边缘增强，核在图像上滑动，乘法和求和值以产生滤波输出。这种数学方法确保各向同性响应，意味着无论边缘在图像中的方向如何，都能一致地检测到。

使用Python和OpenCV的实际实现

实现LoG边缘检测需要设置适当的开发环境与基本库。核心实现依赖于OpenCV进行图像处理操作和NumPy进行数值计算。首先使用pip install opencv-python numpy matplotlib安装这些依赖项。一旦配置完成，实现遵循一个直接的工作流程，从图像加载和预处理开始。

Python实现围绕一个自定义函数，该函数应用高斯模糊后接拉普拉斯算子。关键参数包括kernel_size，它决定模糊操作的邻域大小，以及sigma，控制高斯滤波器的扩展。较大的核大小和较高的sigma值产生更激进的平滑，这对噪声图像有益，但可能损害精细细节的保留。数据类型规范（cv2.CV_64F）确保在拉普拉斯计算期间正确处理负值，这对于后续过程中的准确零交叉检测至关重要。

对于使用各种照片编辑器工具的开发者来说，理解这些底层算法能提供关于专业图像处理软件如何实现其结果的更深见解。使用matplotlib的可视化组件允许对参数调整的即时反馈，促进迭代优化过程。

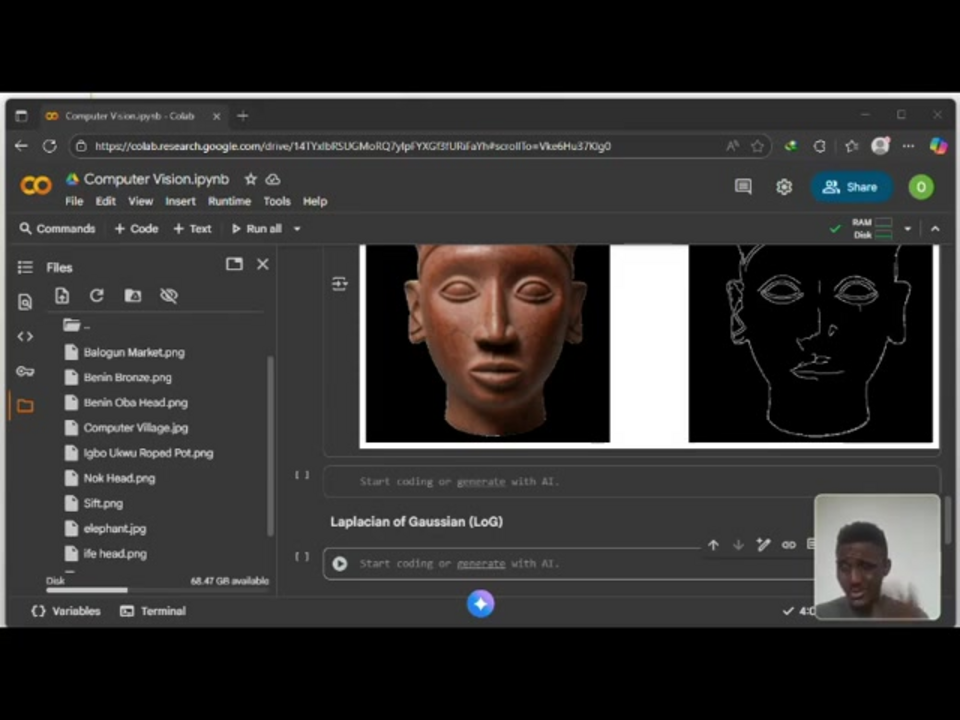
零交叉检测方法

零交叉检测代表LoG边缘检测中最后且最关键的阶段。此过程识别滤波图像在正值和负值之间过渡的精确位置，对应边缘位置。实现涉及扫描LoG处理后的图像，并检查像素邻域以寻找符号变化。一种全面的方法检查多个方向——水平、垂直和两个对角线——以确保不遗漏任何边缘方向。

算法创建一个二进制输出图像，其中检测到的零交叉被标记，而其他区域保持暗色。这种清晰的表示简化了后续处理步骤，并提供了检测边缘的清晰可视化。然而，此过程可能计算密集，特别是对于高分辨率图像，使得优化考虑对于实时应用很重要。诸如邻域修剪和高效内存访问模式等技术可以显著提高性能，而不损害检测准确性。

参数优化策略

成功的LoG实现取决于适当的参数选择，主要是kernel_size和sigma值。这些参数处于微妙的平衡——较大的值增强噪声减少但可能因过度模糊而掩盖真实边缘，而较小的值保留细节但可能不足以抑制噪声。参数调优的系统方法涉及在代表性图像样本上测试多种组合。

对于标准应用，以kernel_size=5和sigma=1.4开始提供了一个合理的基线。具有较高噪声水平的图像可能受益于增加的值（kernel_size=7, sigma=2.0），而高细节图像可能需要更保守的设置（kernel_size=3, sigma=0.8）。最优配置通常取决于特定应用需求，无论是优先边缘精度还是噪声免疫力。许多专业屏幕捕获工具包含类似的参数调整能力，允许用户在处理图像中平衡清晰度和细节。

高级实现考虑

除了基本实现，几个高级考虑可以增强LoG性能。阈值化代表一个有价值的后处理步骤，通过建立最小强度要求来过滤弱边缘。这有助于消除虚假检测，同时保留结构上重要的边缘。此外，形态学操作如膨胀可以连接不连续的边缘片段，创建更连续的边界，更好地表示物体轮廓。

当处理大型图像数据集或在实时环境中操作时，计算效率变得至关重要。优化策略包括使用可分离高斯核，将2D卷积分解为顺序1D操作，显著降低计算复杂性。通过GPU处理或专用图像处理库的硬件加速可以提供显著的性能改进。对于那些使用各种图像转换器应用的人来说，这些优化技术展示了算法效率如何转化为实际性能优势。

实际应用和用例

LoG边缘检测在众多需要精确边界识别的领域中找到应用。在医学成像中，它帮助描绘MRI和CT扫描中的解剖结构，协助诊断和治疗规划。工业检测系统利用LoG通过识别表面图案中的不规则性来检测制造产品中的缺陷。自动驾驶车辆依赖类似的边缘检测技术从相机馈送中解释道路边界和障碍物轮廓。

该方法在科学图像分析中也证明有价值，研究人员从中提取显微图像或天文观测中的特征。即使在创意领域，理解这些算法也增强了与各种图表创建器工具和数字艺术应用的工作。该技术对噪声的鲁棒性使其特别适用于具有挑战性的成像条件，其他方法可能在此失败，确立了LoG作为计算机视觉工具包中的多功能工具。

与其他边缘检测方法的比较

在评估边缘检测技术时，LoG在更简单的基于梯度的方法和更复杂的算法之间占据独特位置。与Sobel或Prewitt等一阶算子相比，LoG提供优越的噪声免疫力但需要更多计算资源。与复杂的Canny边缘检测器相比，LoG提供实现简单性，同时牺牲了Canny的一些灵活性和滞后阈值能力。

方法之间的选择通常取决于特定应用需求。LoG在优先数学优雅、可预测行为和中等噪声抵抗而非终极检测精度的场景中表现出色。其单一算子方法吸引需要直接实现而无需广泛参数调优的应用。对于各种颜色选择器工具的用户来说，理解这些算法差异阐明了软件如何在基础级别提取和处理视觉信息。

优缺点

优点

• 通过高斯预处理实现出色的噪声减少
• 各向同性响应在所有方向平等检测边缘
• 组合算子简化实现工作流程
• 清晰的零交叉表示便于边缘定位
• 平滑和边缘增强之间的有效平衡
• 在多种图像类型和领域中证明可靠
• 数学基础良好，行为可预测

缺点

• 过大核可能导致过度模糊，掩盖精细细节
• 参数敏感性需要仔细调优以获得最佳结果
• 对于高分辨率图像计算密集
• 在复杂场景中可能不如Canny表现好
• 零交叉检测增加处理开销

结论

拉普拉斯高斯边缘检测方法代表了一种复杂的方法，优雅地平衡了噪声减少与精确边缘定位。通过结合高斯平滑和拉普拉斯微分，LoG解决了计算机视觉中的基本挑战，同时保持数学透明度和可预测行为。该技术在医学、工业和研究应用中的多功能性展示了其在图像处理工具包中的持久价值。虽然参数敏感性和计算需求带来实现挑战，但该方法在噪声环境中的鲁棒性能和跨方向的一致边缘检测确保了其持续相关性。随着计算机视觉技术的进步，理解像LoG这样的基础算法为当前能力和自动化图像分析及解释的未来发展提供了关键见解。