Лапласиан Гауссовского обнаружения краев: Руководство по реализации и код на Python

Введение

Обнаружение краев представляет собой фундаментальный столп в компьютерном зрении, позволяя машинам интерпретировать визуальные данные, идентифицируя границы и переходы внутри изображений. Среди доступных сложных техник метод Лапласиана Гаусса (LoG) выделяется своим уникальным подходом к балансировке снижения шума с точной локализацией краев. Это всеобъемлющее руководство исследует математические основы LoG, стратегии практической реализации и техники оптимизации для реальных применений в различных областях, включая медицинскую визуализацию и системы распознавания объектов.

Понимание обнаружения краев Лапласиана Гаусса

Лапласиан Гаусса (LoG) действует как сложный детектор краев второго порядка, который стратегически объединяет две мощные математические операции. Этот двойной подход решает одну из основных проблем в обнаружении краев: различение подлинных особенностей изображения от артефактов случайного шума. Техника начинается с применения гауссова фильтра для сглаживания входного изображения, эффективно подавляя высокочастотный шум, который в противном случае мог бы вызвать ложные обнаружения краев. Этот шаг предварительной обработки создает более чистую основу для последующей операции Лапласиана, которая усиливает области быстрого изменения интенсивности – саму суть краев в цифровой графике.

Что делает LoG особенно эффективным, так это его механизм обнаружения пересечения нуля. После комбинированного процесса фильтрации и дифференцирования алгоритм идентифицирует точки, где обработанные значения изображения переходят от положительных к отрицательным или наоборот. Эти местоположения пересечения нуля точно соответствуют позициям краев в исходном изображении. Эта методология оказывается особенно ценной при работе с изначально зашумленными источниками данных, такими как медицинские сканы или фотографии при слабом освещении, где традиционные детекторы краев могут бороться с точностью. Для тех, кто исследует различные генераторы изображений ИИ, понимание этих фундаментальных техник компьютерного зрения предоставляет ценное понимание того, как искусственный интеллект обрабатывает визуальную информацию.

Математическая основа LoG

Математическая элегантность LoG заключается в комбинации двух хорошо установленных операций. Компонент гауссовой фильтрации использует двумерную гауссову функцию, определяемую как G(x, y) = (1/(2πσ²)) × e^(-(x²+y²)/(2σ²)), где σ представляет стандартное отклонение, контролирующее степень сглаживания. Это гауссово ядро создает взвешенное среднее окрестностей пикселей, причем ближайшие пиксели вносят более значительный вклад в результат, чем удаленные.

Оператор Лапласиана затем применяет дифференцирование второго порядка к этому сглаженному изображению. Математически выражаемое как ∇²f = ∂²f/∂x² + ∂²f/∂y², эта операция выделяет области, где интенсивность изменяется быстро. Комбинированное ядро LoG возникает как Лапласиан гауссовой функции: LoG(x, y) = ∇²G(x, y) = -(1/(πσ⁴)) × [1 - (x²+y²)/(2σ²)] × e^(-(x²+y²)/(2σ²)). Это сложное ядро одновременно выполняет сглаживание и усиление краев через свертку, где ядро скользит по изображению, умножая и суммируя значения для получения отфильтрованного выхода. Этот математический подход обеспечивает изотропный отклик, означающий, что края обнаруживаются последовательно независимо от их ориентации в изображении.

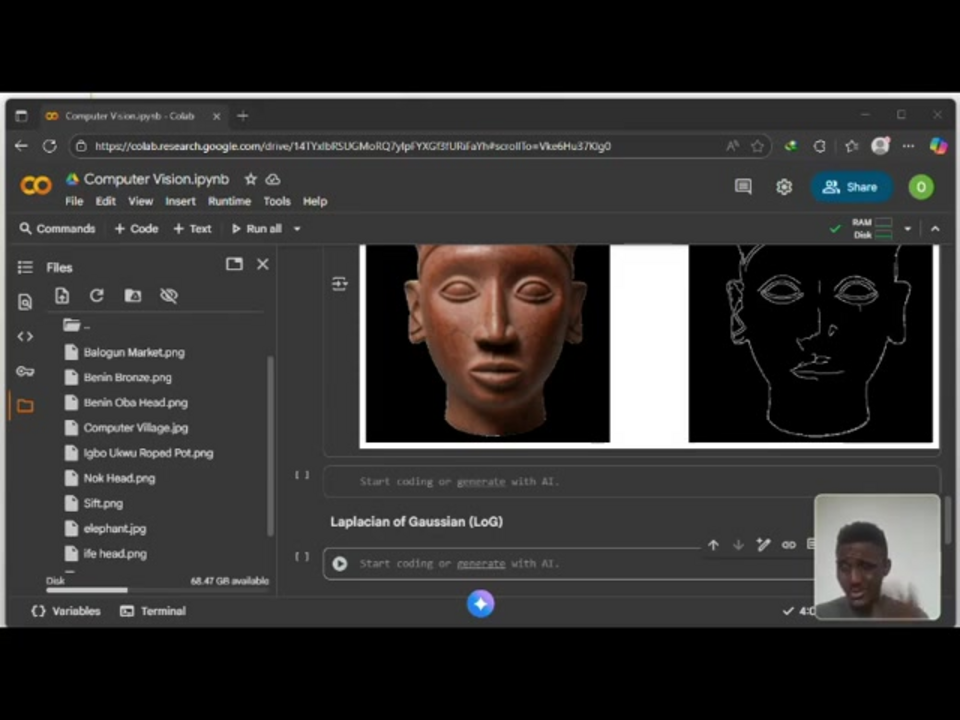
Практическая реализация с Python и OpenCV

Реализация обнаружения краев LoG требует настройки правильной среды разработки с необходимыми библиотеками. Основная реализация опирается на OpenCV для операций обработки изображений и NumPy для численных вычислений. Начните с установки этих зависимостей, используя pip install opencv-python numpy matplotlib. После настройки реализация следует прямому рабочему процессу, который начинается с загрузки изображения и предварительной обработки.

Реализация на Python сосредоточена вокруг пользовательской функции, которая применяет гауссово размытие с последующим оператором Лапласиана. Критические параметры включают kernel_size, который определяет размер окрестности для операций размытия, и sigma, контролирующий распространение гауссова фильтра. Большие размеры ядра и более высокие значения sigma производят более агрессивное сглаживание, что полезно для зашумленных изображений, но может скомпрометировать сохранение мелких деталей. Спецификация типа данных (cv2.CV_64F) обеспечивает правильную обработку отрицательных значений во время вычисления Лапласиана, что необходимо для точного обнаружения пересечения нуля позже в процессе.

Для разработчиков, работающих с различными редакторами фотографий, понимание этих основных алгоритмов предоставляет более глубокое понимание того, как профессиональное программное обеспечение для обработки изображений достигает своих результатов. Компонент визуализации с использованием matplotlib позволяет получить немедленную обратную связь по корректировкам параметров, облегчая итерационный процесс оптимизации.

Методология обнаружения пересечения нуля

Обнаружение пересечения нуля представляет собой финальную и наиболее критическую фазу в обнаружении краев LoG. Этот процесс идентифицирует точные местоположения, где отфильтрованное изображение переходит между положительными и отрицательными значениями, соответствующими позициям краев. Реализация включает сканирование обработанного LoG изображения и исследование окрестностей пикселей на предмет изменений знака. Всесторонний подход проверяет несколько направлений – горизонтальное, вертикальное и обе диагонали – чтобы гарантировать, что ни одна ориентация края не пропущена.

Алгоритм создает бинарное выходное изображение, где обнаруженные пересечения нуля отмечены, в то время как другие области остаются темными. Это чистое представление упрощает последующие шаги обработки и предоставляет четкую визуализацию обнаруженных краев. Однако этот процесс может быть вычислительно интенсивным, особенно для изображений высокого разрешения, что делает соображения оптимизации важными для приложений реального времени. Техники, такие как обрезка окрестностей и эффективные шаблоны доступа к памяти, могут значительно улучшить производительность без компромисса точности обнаружения.

Стратегии оптимизации параметров

Успешная реализация LoG зависит от соответствующего выбора параметров, в основном значений kernel_size и sigma. Эти параметры находятся в деликатном балансе – большие значения усиливают снижение шума, но рискуют чрезмерным размытием, которое скрывает подлинные края, в то время как меньшие значения сохраняют детали, но могут недостаточно подавлять шум. Систематический подход к настройке параметров включает тестирование нескольких комбинаций на репрезентативных образцах изображений.

Для стандартных применений, начало с kernel_size=5 и sigma=1.4 предоставляет разумный базовый уровень. Изображения с более высокими уровнями шума могут выиграть от увеличенных значений (kernel_size=7, sigma=2.0), в то время как изображения с высокой детализацией могут потребовать более консервативных настроек (kernel_size=3, sigma=0.8). Оптимальная конфигурация часто зависит от конкретных требований приложения, будь то приоритет точности краев или иммунитета к шуму. Многие профессиональные инструменты захвата экрана включают аналогичные возможности корректировки параметров, позволяя пользователям балансировать ясность и детали в их обработанных изображениях.

Расширенные соображения реализации

Помимо базовой реализации, несколько расширенных соображений могут улучшить производительность LoG. Пороговая обработка представляет собой ценный шаг постобработки, который фильтрует слабые края, устанавливая минимальные требования к интенсивности. Это помогает устранить ложные обнаружения, сохраняя структурно значимые края. Дополнительно, морфологические операции, такие как дилатация, могут соединять прерывистые фрагменты краев, создавая более непрерывные границы, которые лучше представляют контуры объектов.

Вычислительная эффективность становится решающей при обработке больших наборов данных изображений или работе в средах реального времени. Стратегии оптимизации включают использование разделяемых гауссовых ядер, которые разлагают 2D свертку в последовательные 1D операции, значительно снижая вычислительную сложность. Аппаратное ускорение через GPU обработку или специализированные библиотеки обработки изображений может предоставить существенные улучшения производительности. Для тех, кто работает с различными конвертерами изображений, эти техники оптимизации демонстрируют, как алгоритмическая эффективность переводится в практические преимущества производительности.

Реальные применения и случаи использования

Обнаружение краев LoG находит применение во многочисленных областях, где точная идентификация границ является решающей. В медицинской визуализации это помогает очерчивать анатомические структуры в МРТ и КТ сканах, помогая в диагностике и планировании лечения. Промышленные системы инспекции используют LoG для обнаружения дефектов в изготовленных продуктах, идентифицируя нерегулярности в поверхностных узорах. Автономные транспортные средства полагаются на аналогичные техники обнаружения краев для интерпретации границ дороги и контуров препятствий из потоков камер.

Методология также оказывается ценной в научном анализе изображений, где исследователи извлекают особенности из микроскопических изображений или астрономических наблюдений. Даже в творческих областях понимание этих алгоритмов улучшает работу с различными инструментами создания диаграмм и приложениями цифрового искусства. Устойчивость техники к шуму делает ее особенно подходящей для сложных условий визуализации, где другие методы могут потерпеть неудачу, устанавливая LoG как универсальный инструмент в наборе компьютерного зрения.

Сравнение с альтернативными методами обнаружения краев

При оценке техник обнаружения краев LoG занимает отличительную позицию между более простыми градиентными методами и более сложными алгоритмами. По сравнению с операторами первого порядка, такими как Собеля или Преввитта, LoG предоставляет превосходный иммунитет к шуму, но требует больше вычислительных ресурсов. По сравнению с сложным детектором краев Кэнни, LoG предлагает простоту реализации, жертвуя некоторой гибкостью Кэнни и возможностями гистерезисной пороговой обработки.

Выбор между методами часто зависит от конкретных требований приложения. LoG преуспевает в сценариях, где математическая элегантность, предсказуемое поведение и умеренная устойчивость к шуму приоритетны над абсолютной точностью обнаружения. Его подход с одним оператором привлекателен для приложений, требующих прямолинейной реализации без обширной настройки параметров. Для пользователей различных инструментов выбора цвета, понимание этих алгоритмических различий освещает, как программное обеспечение извлекает и обрабатывает визуальную информацию на фундаментальных уровнях.

Плюсы и минусы

Преимущества

• Отличное снижение шума через гауссову предварительную обработку
• Изотропный отклик обнаруживает края во всех ориентациях одинаково
• Комбинированный оператор упрощает рабочий процесс реализации
• Четкое представление пересечения нуля облегчает локализацию краев
• Эффективный баланс между сглаживанием и усилением краев
• Доказанная надежность в разнообразных типах изображений и областях
• Математически обоснованный с предсказуемым поведением

Недостатки

• Чрезмерное размытие может скрыть мелкие детали с большими ядрами
• Чувствительность к параметрам требует тщательной настройки для оптимальных результатов
• Вычислительно интенсивный для изображений высокого разрешения
• Может уступать по производительности Кэнни в сложных сценариях
• Обнаружение пересечения нуля добавляет накладные расходы на обработку

Заключение

Метод обнаружения краев Лапласиана Гаусса представляет собой сложный подход, который элегантно балансирует снижение шума с точной локализацией краев. Через комбинацию гауссова сглаживания и дифференцирования Лапласиана, LoG решает фундаментальные вызовы в компьютерном зрении, сохраняя математическую прозрачность и предсказуемое поведение. Универсальность техники в медицинских, промышленных и исследовательских применениях демонстрирует ее непреходящую ценность в наборе обработки изображений. Хотя чувствительность к параметрам и вычислительные требования представляют проблемы реализации, устойчивая производительность метода в зашумленных средах и последовательное обнаружение краев во всех ориентациях обеспечивают его продолжающуюся актуальность. По мере развития технологий компьютерного зрения понимание фундаментальных алгоритмов, таких как LoG, предоставляет решающее понимание как текущих возможностей, так и будущих разработок в автоматизированном анализе и интерпретации изображений.